Il teorema di Shannon-Hartley indica la velocità massima alla quale le informazioni possono essere trasmesse su un canale di comunicazione di una larghezza di banda specificata in presenza di rumore.
Il Teorema di Shannon dà un limite superiore alla capacità di un canale, in bit per secondo (bps), in funzione della larghezza di banda disponibile e il rapporto segnale-rumore del collegamento.
Il teorema può essere indicato come:
C = B * log2 (1 + S/N)
dove C è la capacità del canale realizzabile, B è la banda della linea, S è la potenza media del segnale e N è la potenza media del rumore.
Il rapporto segnale-rumore (S/N) è generalmente espresso in decibel (dB) dato dalla formula:
10 * log10 (S/N)
così per esempio un rapporto segnale-rumore di 1000 è comunemente espressa come:
10 * log10 (1000) = 30 dB.
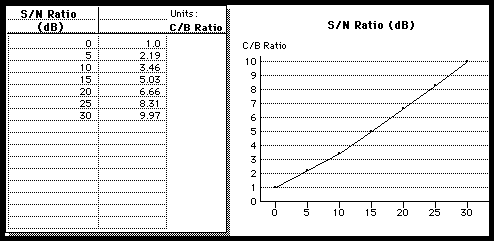
Qui è un grafico che mostra la relazione tra C/B e S/N (in dB):
Ecco due esempi di uso del teorema di Shannon.
1) MODEM
Per una tipica linea telefonica con un rapporto segnale-rumore di 30dB e una larghezza di banda audio di 3 kHz, si ottiene una velocità di trasferimento dati massima di:
C = 3000 * log2 (1001)
che è un po ‘inferiore a 30 kbps.
2) TV satellitare Canale
Per un canale TV satellitare con un segnale-rumore di 20 dB e una larghezza di banda video di 10 MHz, si ottiene una velocità di trasferimento dati massima di:
C = 10000000 * log2 (101) che è di circa 66 Mbps.
LL Peterson e BS Davie, Reti di calcolatori: un approccio di sistema (Morgan Kaufmann), 1996. ISBN: 1-55860-368-9 (Brossura ISBN: 1-55860-404-9), pp 94-95.